Ce este durata modificată?
Durata modificată îi spune investitorului cât de mult se va schimba prețul obligațiunii, având în vedere modificarea randamentului acesteia. Deoarece lumea obligațiunilor este mai complexă decât lumea acțiunilor, este important ca investitorul să cunoască durata modificată a obligațiunii. Pentru a calcula mai întâi durata modificată a obligațiunii, investitorul trebuie să mai calculeze încă un lucru, care este durata Macauley. Pentru a calcula durata Macauley, investitorul trebuie să-și dea seama care este momentul fluxului de numerar
Formula de durată modificată
Deci, formula pentru Durata modificată este pur și simplu.
Durata modificată = Durata Maculay / (1 + YTM / n)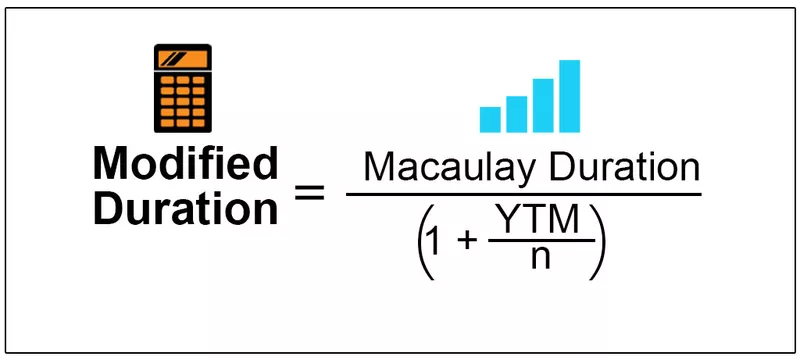
Unde,
- Durata Macauley = Durata calculează timpul mediu ponderat înainte ca obligațiunea să primească fluxurile de numerar ale obligațiunii. Durata modificată este ordonată să fie calculată mai întâi. Investitorul trebuie să calculeze durata Macauley a obligațiunii.
- YTM = Randamentul până la scadență este pur și simplu randamentul total pe care investitorul l-ar câștiga într-o obligațiune atunci când obligațiunea este deținută până la scadență
- N = numărul de perioade de cupon pe an
Calculul duratei modificate cu exemple
Exemplul nr. 1
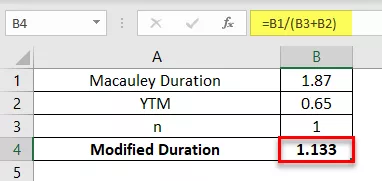
O plată anuală de 2 ani a obligațiunii de 5.000 USD are o durată Macaulay de 1,87 ani. YTM al obligațiunii este de 6,5%. Calculați durata modificată a obligațiunii.
Exemplul nr. 2
O plată anuală de 2 ani a obligațiunii de 2.000 USD are o durată Macaulay de 2 ani. YTM al obligațiunii este de 5%. Calculați durata modificată a obligațiunii.

Exemplul nr. 3
O plată anuală de 4 ani a obligațiunii de 12.000 USD are o durată Macaulay de 5,87 ani. YTM al obligațiunii este de 4,5%. Calculați durata modificată a obligațiunii.

Exemplul # 4
O plată anuală de 5 ani a obligațiunii de 11.000 $ are o durată Macaulay de 1,5 ani. YTM al obligațiunii este de 7%. Calculați durata modificată a obligațiunii.

Avantaje
- Principalul avantaj este că investitorul trebuie să cunoască durata obligațiunii, deoarece volatilitatea prețului obligațiunii este direct legată de prețurile obligațiunilor. Cu cât durata obligațiunii este mai mare, cu atât volatilitatea prețului este mai mare
- Durata oricărui instrument de investiții poate ajuta la gestionarea unor nevoi mai bune de investiții pentru viitor, deoarece investitorul poate planifica în mod eficient cursul viitor al investiției sale pe durata
- Este, de asemenea, o măsură a riscului obligațiunii la schimbare și a randamentului din prețul obligațiunii
- Durata medie a fondului este, de asemenea, importantă, deoarece vă spune cât de sensibil va fi fondul la modificările ratelor dobânzii de pe piață
Dezavantaje
- Calculul duratei modificate este de natură complexă datorită calculului Duratei Macaulay, iar apoi utilizatorul sau investitorul are nevoie și de intrările de randament și de funcționare a calculului duratei modificate
- Obținerea unor date care sunt corecte și care prevalează pe piață este greu de realizat, deoarece fluctuațiile prețurilor și prețurile pieței se schimbă în fiecare minut, ceea ce face calculul incorect și învechit
- Durata nu este, de asemenea, o măsură completă a riscului conținut în prețul obligațiunii și durata obligațiunii. Investitorul nu poate să se bazeze exclusiv pe măsura duratei pentru a produce măsuri precise de risc
- Durata Macaulay calculează durata medie ponderată a obligațiunii, care nu este de fiecare dată o măsură bună a riscului în obligațiune
Concluzie
Modificat și Macaulay, deși a avea limitări este într-adevăr un concept foarte util, în special pentru managerii de portofoliu pentru a măsura volatilitatea obligațiunii și riscul asociat cu aceasta, prin urmare poate servi ca un instrument foarte util atunci când managerul construiește un portofoliu de obligațiuni și gestionarea riscului asociat acestuia.