PV = L * (1 - (1 + r) -n / r)
Unde- PV este valoarea actualizată a soldului restant
- L este plata existentă
- r este rata dobânzii
- n este frecvența plăților
Calculator de plată a datoriilor
Calculatorul de plată a datoriilor este un tip de calculator în care, dacă împrumutatul dorește să consolideze împrumuturile restante și să încerce să le plătească rapid pentru a reduce povara dobânzii și ieșirea excesivă a sumei.
Despre Calculatorul de plată a datoriilor
Mai întâi, aflați valoarea actuală a soldurilor restante pe împrumuturile multiple.
PV = L * (1 - (1 + i) -n / r)Următorul ar fi să aflăm noua sumă a ratei, care ar putea fi fie suma valorii ratei existente, cât și plata suplimentară, dacă se va face vreuna.
Acum calculați perioada în care datoria poate fi achitată
nPVA = ln ((1 - PV (i) / L ') -1) ) / ln (1 + i)Unde
- PV este valoarea actualizată a soldului restant
- L este plata existentă
- L 'este noua plată
- i este rata dobânzii
- n este frecvența plăților
- nPVA este numărul de plăți periodice
Este un calculator la îndemână, deoarece va calcula care va fi proprietatea atunci când toate datoriile sunt achitate. În acest caz, împrumutatul poate sta cu mai multe împrumuturi cu dobânzi diferite și este dispus să le consolideze. Mai mult, împrumutatul ar putea chiar să dorească să crească periodic rata ratei sau să consolideze și suma ratei. Acest lucru îl va ajuta să reducă povara dobânzii și, de asemenea, să îndepărteze datoria devreme. Decizia nu este la fel de ușoară pe cât a cerut creșterea sumei rate, ceea ce ar putea crește povara asupra fluxului de numerar al debitorului. Acest calculator va ajuta să calculeze numai în ce perioadă de timp pot achita datoria în totalitate atunci când datoriile sunt consolidate.
Cum se calculează utilizând calculatorul de rambursare a datoriilor?
Trebuie să urmați pașii de mai jos pentru a calcula proprietatea datoriilor consolidate.
Pasul 1 - Mai întâi, împrumutatul trebuie să stabilească care este soldul curent al datoriei, care nu este altceva decât să afle valoarea actuală a datoriei.
Pasul 2 - Determinați acum noua sumă a ratei, care este suma ratei ratei existente pe care o plătește în prezent și suma suplimentară pe care debitorul se gândește să o înceapă.
Pasul 3 - Aflați împrumutul, care are dobânzi mai mari și clar că datoriile se plătesc mai întâi și continuă să plătească suma minimă sau în rate pentru alte împrumuturi restante.
Pasul 4 - Acum calculați principalul restant la creditele rămase și calculați durata de împrumut cu noua sumă ratată.
Pasul 5 - Dreptul rezultat poate fi convertit în ani împărțind valoarea ajunsă la pasul 4 la 12, iar cifrele din partea dreaptă a zecimalului pot fi înmulțite cu 12 pentru a le obține în luni.
Exemplu
Domnul X are două împrumuturi restante, unul este un împrumut auto, iar altul este un credit ipotecar.
Detaliile ambelor împrumuturi sunt date mai jos:

Managerul sucursalei l-a abordat pe domnul X cu o schemă prin care poate consolida împrumuturile restante în prezent și poate achita datoria mai devreme. Bancherul i-a furnizat detaliile schemei care urmau să plătească mai întâi datoria mai mare și apoi să continue suma fixă a împrumutului închis care urmează să fie rambursat pe creditul ipotecar, ceea ce îi va reduce durata de închidere a împrumutului. Domnul X a fost de asemenea de acord să mărească suma ratei cu 200 USD, consolidând în același timp împrumuturile restante și va continua să facă acest lucru până la achitarea datoriilor.
Vi se cere să calculați proprietatea cu care va fi achitată datoria.
Soluţie:
Trebuie să calculăm valoarea actualizată a soldului datoriilor curente restante, care poate fi calculată conform formulei de mai jos:
Imprumut auto
Rata dobânzii aplicabilă lunar = 8/12 = 0,67%
Perioada rămasă va fi (7 * 12) - (3 * 12), care este 84 - 36, adică 48.
PV = L * (1 - (1 + i) -n / r)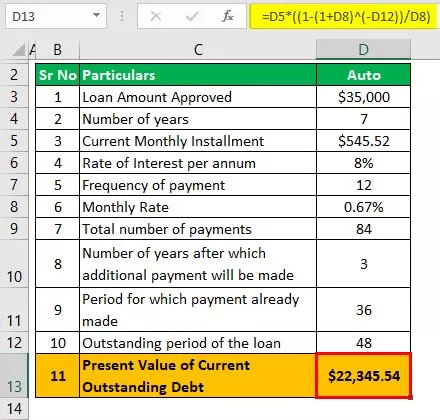
- = 545 USD. 52 * (1 - (1 + 0,67%) -48 ) / 0,67%)
- = 22.345,54 dolari
Credit ipotecar
Rata dobânzii aplicabilă lunar = 5/12 = 0,42%
Perioada rămasă va fi (25 * 12) - (10 * 12), adică 300 - 120, adică 180.
PV = L * (1 - (1 + i) -n / r)
- = 1.227,64 USD * (1 - (1 + 0,42%) -180 / 0,42%)
- = 155.241,51 dolari
Împrumut restant consolidat

- = 22.345,44 USD + 155.241,40 USD
- = 177.586,84 dolari
Ni se oferă aici, rata lunară existentă pe care o plătește pentru un împrumut auto este de 545,52 USD, iar suma existentă pentru un credit ipotecar este de 1.227,64 USD. Suma consolidată a ratei ar fi de 1.773,16 USD, iar dl X dorește, de asemenea, să crească această sumă cu 200 USD. Prin urmare, suma totală a ratei noi ar fi de 1.973,16 USD
În primul rând, suma în rate a împrumutului Auto va fi achitată din momentul în care are dobânzi mai mari, iar noua sumă care ar fi utilizată pentru achitarea împrumutului auto ar fi de 545,52 USD + 200 USD, care este 745,52 USD, iar suma restului va fi utilizată pentru a plăti Off credit ipotecar, care este de 1.973,16 USD - 745,52 USD, care este egal cu 1.227,64 USD
Acum, vom calcula în ce interval de timp va fi eliminat împrumutul auto
nPVA = ln ((1 - PV (i) / L ') -1) ) / ln (1 + i)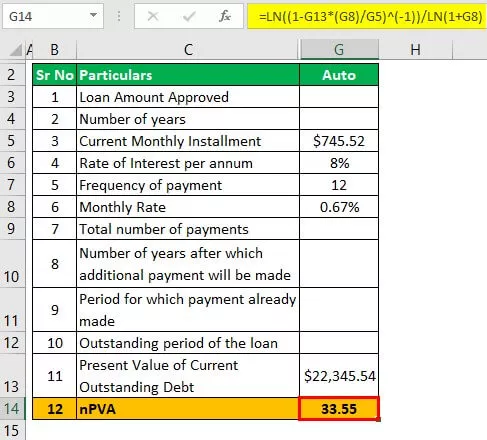
- = ln (((1- 22.345,44 * (0,67%) / 745,52) -1 ) / ln (1 + 0,67%)
- = 33,55
În prezent, proprietatea restantă a creditului ipotecar ar fi cu 180 mai puțin 33,55, adică 146,45
Împrumutul ipotecar după ce împrumutul auto este plătit
Rata dobânzii aplicabilă lunar = 5/12 = 0,42%
PV = L * (1 - (1 + i) -n / r)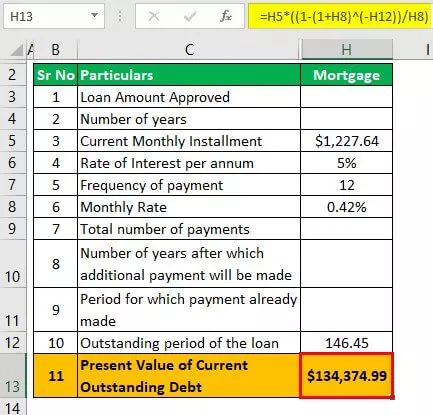
- = 1.227,64 USD * (1 - (1 + 0,42%) -146,45 / 0,42%)
- = 134.374,99 dolari
Acum, vom calcula în ce interval de timp va fi eliberat împrumutul ipotecar
nPVA = ln ((1 - PV (i) / L ') -1 ) / ln (1 + i)
- = ln (((1- 134,374,92 * (0,42%) / 1,973,16) -1 ) / ln (1 + 0,42%)
- = 80,26
Prin urmare, proprietatea totală în cadrul căreia împrumutul poate fi compensat este de 33,55 + 80,26, adică 113,81 și atunci când se împarte același lucru la 12, adică 9,48 ani, adică în 9 ani și 6 luni.








